Rational numbers introduction, exercises and answers

Rational numbers

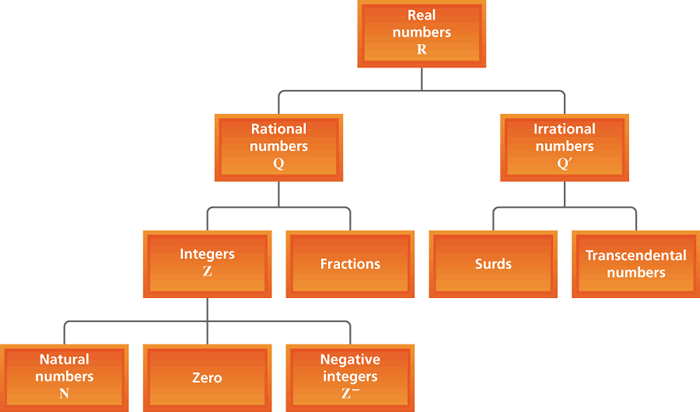
A rational number is a number that can be written as a fraction. Rational numbers are all real numbers, and can be positive or negative. We use the letter Q to represent this set of numbers.

diagram

Adding or subtracting rational numbers

We can only add or subtract rational numbers if they have the same denominator. This is usually the lowest common multiple of all the denominators in the question. Change any mixed numerals to improper fractions before adding or subtracting them.

Example 1

Solution

Evaluate $\frac{5}{7}$ + $4 \frac{3}{5}$ − $2 \frac{2}{3}$ .

$\frac{5}{7}$ + 4 $\frac{3}{5}$ − 2 $\frac{2}{3}$

= $\frac{5}{7}$ + $\frac{23}{5}$ − $\frac{8}{3}$

= $\frac{75}{105}$ + $\frac{483}{105}$ − $\frac{280}{105}$

= $\frac{278}{105}$

= 2 $\frac{68}{105}$

Multiplying or dividing rational numbers

Hint

■ The reciprocal of a fraction is obtained by interchanging the numerator and the denominator, i.e. inverting the fraction.

You can multiply rational numbers by multiplying the numerators together and the denominators together. It is easier to change any mixed numbers to improper fractions and cancel down before multiplying.

To divide rational numbers, you need to turn the second fraction (the one you want to divide by) upside down. You can then multiply the first fraction by the reciprocal.

Example 2

Solution

Evaluate 3 $\frac{1}{5}$ × 1 $\frac{1}{4}$ ÷ 1 $\frac{2}{3}$ .

3 $\frac{1}{5}$ × 1 $\frac{1}{4}$ ÷ 1 $\frac{2}{3}$

= $\frac{16}{5}$ × $\frac{5}{4}$ ÷ $\frac{5}{3}$

= $\frac{{}^{4}16}{{}_{1}5}$ × $\frac{{}^{1}5}{{}_{1}4}$ × $\frac{3}{5}$

= $\frac{4}{1}$ × $\frac{1}{1}$ × $\frac{3}{5}$

= 2 $\frac{2}{5}$

Finite and recurring decimals

The set of rational numbers includes finite decimals and recurring decimals.

A finite decimal (or terminating decimal) is a decimal number that stops after a few decimal places. For example, 2.87 is a finite decimal.

A recurring decimal is a decimal number that repeats with a regular pattern.

3.666 66… is a recurring decimal and this can be written as $3 . \dot{6}$

5.252 525… is a recurring decimal and this can be written as $5 . \dot{2} \dot{5}$ or $5 . \bar{25}$ .

Example 3

Solution

Write 2.68 as a fraction in simplest form.

2.68	= $\frac{2}{1}$ + $\frac{6}{10}$ + $\frac{8}{100}$ = $\frac{268}{100}$

Example 4

Solution

Write $2 . \dot{6}$ as fraction in simplest form.

$2 . \dot{6}$ = 2 + $0 . \dot{6}$

Let x

10x

= $0 . \dot{6}$ = 0.666 6…

= $6 . \dot{6}$ = 6.666 6…

So	10x	= 6.666 6…
	− x	= 0.666 6…
	9x	= 6

x = $\frac{6}{9}$ = $\frac{2}{3}$

$2 . \dot{6}$

= 2 + $0 . \dot{6}$

= 2 $\frac{2}{3}$ or $\frac{8}{3}$

Answers

Exercise

1 Calculate:

a $\frac{3}{5}$ + $\frac{2}{9}$	b $\frac{4}{7}$ − $\frac{3}{10}$	c $\frac{3}{4}$ + $\frac{5}{6}$ − $\frac{6}{7}$
d 2 $\frac{6}{25}$ + $\frac{4}{9}$	e 2 $\frac{1}{6}$ − 1 $\frac{3}{4}$	f 2 $\frac{3}{4}$ − 1 $\frac{5}{8}$ + 3 $\frac{7}{12}$

2 Calculate:

a $\frac{4}{7}$ ÷ $\frac{16}{21}$	b $\frac{3}{5}$ + $\frac{2}{9}$	c 1 $\frac{5}{9}$ × 5 $\frac{4}{7}$
d 3 $\frac{1}{8}$ ÷ 2 $\frac{1}{2}$	e 1 $\frac{5}{14}$ ÷ 1 $\frac{12}{15}$ × 3 $\frac{35}{38}$	f $\frac{2}{5}$ ÷ 1 $\frac{5}{16}$ + 3 $\frac{1}{2}$

3 Use BODMAS to calculate:

a $\frac{5}{16} (\frac{3}{4} + \frac{7}{8})$	b $\frac{3}{4} (3 \frac{1}{2} - \frac{2}{3})$	c $1 \frac{5}{8} \times 2 \frac{1}{2} - 3 \frac{1}{5} \times 1 \frac{3}{4}$
d $\frac{3}{4}$ − $\frac{1}{2}$ × $\frac{2}{3}$ + 2 $\frac{1}{5}$	e 2 $\frac{1}{2}$ ÷ $\frac{3}{4}$ × 1 $\frac{1}{3}$ − 2 $\frac{5}{8}$	f $(\frac{3}{7} + \frac{4}{5})$ ÷ 2 $\frac{1}{8}$

4 Let a = $\frac{3}{4}$ , b = −1 $\frac{1}{2}$ , c = 2 $\frac{3}{4}$ and d = − $\frac{1}{6}$ . Find:

a ab − cd	b a × d − b ÷ c	c 2a + 3d − c
d 3a − 2b ÷ 5d	e a + 2b + $\frac{1}{2}$	f 3 − d(c + b)
g a(c − d)	h c − $\frac{1}{3}$ d − $\frac{5}{6}$	i 6(d + 4) + 2

5 Write the following terminating decimals as fractions in simplest form.

a 0.5275

b 3.124

c 7.950

d 53.275

6 Write the following recurring decimals as fractions in simplest form.

a $0 . \dot{7}$

b $0 . \bar{12}$

c $3 . \dot{6} \dot{1}$

d $1 . \bar{581}$

cartoon